Question

a sample of radioactive isotope had an initial mass of 800 mg in the year 2000 and decays exponentially better over time. a measurement in the year 2005 found that the sample’s mass had decayed to 190 mg. what would be the expected mass of the sample in the year 2009, to the nearest whole number?

Answer 1

The expected mass of the sample in the year 2009 is approximately 60 miligrams.

Explanation:

The mass of radioactive isotopes decays exponentially in time, the equation that represents this phenomenon is presented below:

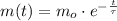`m(t) = m_(o)\cdot e^{-(t)/(\tau) }` (1)

Where:

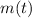`m(t)` - Current mass of the radioactive isotope, in miligrams.

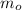`m_(o)` - Initial mass of the radioactive isotope, in miligrams.

`t` - Time, in years.

`\tau` - Time constant, in years.

First, we must find the time constant associated to the decay of the radioactive isotope by clearing the respective term in (1):

`-(t)/(\tau) = \ln (m(t))/(m_(o))`

`\tau = -(t)/(\ln (m(t))/(m_(o)) )`

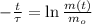
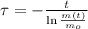
If we know that
`t = 5\,y`,
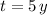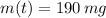`m(t) = 190\,mg` and
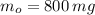`m_(o) = 800\,mg`, then the time constant is:

`\tau = -(t)/(\ln (m(t))/(m_(o)) )`

`\tau = -(5\,y)/(\ln (190\,mg)/(800\,mg) )`

`\tau \approx 3.478\,y`

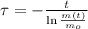
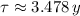
Now, we calculate the mass of the radioactive isotope in 2009 (
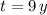`t = 9\,y`). If we know that
`t = 9\,y`,
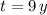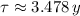`\tau \approx 3.478\,y` and
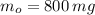`m_(o) = 800\,mg`, then the mass of the radioactive isotope is:

`m(t) = m_(o)\cdot e^{-(t)/(\tau) }`

`m(9\,y) = (800\,mg)\cdot e^{-(9\,y)/(3.478\,y) }`

`m(9\,y) \approx 60.155\,mg`

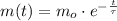
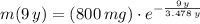
The expected mass of the sample in the year 2009 is approximately 60 miligrams.