Answer:
The maximum profit of $847.03 occurs when Melissa produces 25 soaps and 25 candles.
Step-by-step explanation:
The linear programming equations forms as follows:
Cost of producing 1 Soap=Cost of Soap Base+Cost of Coconut Oil+Cost of Essential Oil
Cost of Soap base is $2.
Cost of Coconut Oil for one soap is
 .
.
Cost of Essential Oil for one soap is
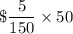
So the total cost of 1 soap is
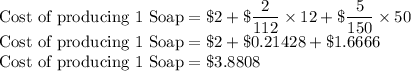
So the cost of producing one bar of soap is 3.8808
So the profit per soap is
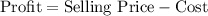
Here selling price is $18 for soap so
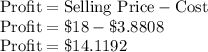
Profit per soap is $14.1192.
Similarly the cost of producing 1 candle is as follows:
Cost of producing 1 Candle=Cost of Wax Base+Cost of Coconut Oil+Cost of Essential Oil
Cost of Wax base is $2.25.
Cost of Coconut Oil for one candle is
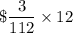 .
.
Cost of Essential Oil for one candle is
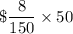
So the total cost of 1 candle is
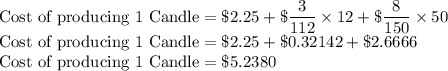
So the cost of producing one candle is $35.2380
So the profit per candle is
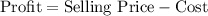
Here selling price is $25 for a candle so
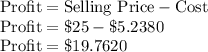
Profit per candle is $19.7620.
If the number of soaps produced is X and the number of candles produced is Y then the maximization function of profit is given as
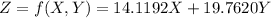
Also the constraints are given as follows:
If Melissa has 3 jars of coconut oil and each jar has 112 tablespoons thus the total tablespoons Melissa has are 336. If 2 tablespoon coconut oil is used for 1 soap and 3 tablespoons are used for 1 candle thus

Similarly, Melissa has 2.5 containers of essential oil and each container has 150 drops thus the total drops Melissa has are 375. If 5 drops of essential oil are used for 1 soap and 8 drops are used for 1 candle thus
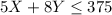
For the soap bases, each soap uses 1 soap bases and total soap bases are 25 thus
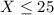
Similarly, for the wax base, each candle uses 1 wax base, and the total wax bases are 25 thus.

So the linear programming model becomes
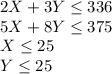
with maximization of
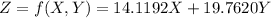
Now solving this using the graphical method of linear programming as attached gives:
The maximum profit of 847.03 occur when Melissa produces 25 soaps and 25 candles.