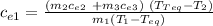Question

You leave a pastry in the refrigerator on a plate and ask your roommate to take it out before youget home so you can eat it at room temperature, the way you like it. Instead, your roommateplays video games for hours. When you return, you notice that the pastry is still cold, but thegame console has become hot. Annoyed, and knowing that the pastry will not be good if it ismicrowaved, you warm up the pastry by unplugging the console and putting it in a clean trashbag (which acts as a perfect calorimeter) with the pastry on the plate. After a while, you find thatthe equilibrium temperature is a nice, warmTeq.. You know that the game console has a mass ofm1. Approximate it as having a uniform initial temperature ofT1. The pastry has a mass ofm2and a specific heat ofc2, and is at a uniform initial temperature ofT2. The plate is at the sameinitial temperature and has a mass ofm3and a specific heat ofc3. What is the specific heat ofthe console

Answer 1

`c_(e1) = ((m_2 c_(e2) \ + m_3 c_(e3) ) \ (T_(Teq) - T_2) )/(m_1 (T_1 - T_(eq)) )`

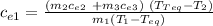
Step-by-step explanation:

This is a calorimeter problem where the heat released by the console is equal to the heat absorbed by the cupcake and the plate.

Q_c = Q_{abs}

where the heat is given by the expression

Q = m c_e ΔT

m₁ c_{e1) (T₁-T_{eq}) = m₂ c_{e2} (T_{eq} -T₂) + m₃ c_{e3} (T_{eq}- T₁)

note that the temperature variations have been placed so that they have been positive

They ask us for the specific heat of the console

`c_(e1) = ((m_2 c_(e2) \ + m_3 c_(e3) ) \ (T_(Teq) - T_2) )/(m_1 (T_1 - T_(eq)) )`