Question

brandon took a 50-question exam worth a total of 160 points. There were x two-point questions and y five point questions. How many of each type of question were on the exam?

Answer 1

`\large{\boxed{\sf x = 30 , \ y \ = \ 20}}`

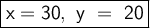
Explanation:

Here it is given that Brandon took a 50 question exam worth of 160points . So here the sum of 2 point and 5 point question is 50. So ,

`\sf\qquad\longrightarrow x + y = 50.....(i)`

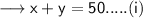
Again the maximum marks for the exam is 160 . Therefore ,

`\sf\qquad\longrightarrow 2x + 5y = 160 ..... (ii)`

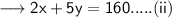
Multiply equation (i) with 5 ,

`\sf\qquad\longrightarrow 5x + 5y = 250`

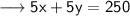
Subtract equation (ii) and (i) ,

`\sf\qquad\longrightarrow 5x - 2x = 250-160\\`

`\sf\qquad\longrightarrow 3x = 90\\`

`\sf\qquad\longrightarrow x =(90)/(3)\\`

`\sf\qquad\longrightarrow \pink{ x = 30}`

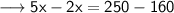
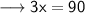
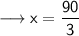
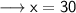
Substitute this value in (i) ,

`\sf\qquad\longrightarrow y = 50-x \\`

`\sf\qquad\longrightarrow y= 50-30\\`

`\sf\qquad\longrightarrow \pink{ y = 20}`

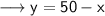
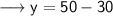
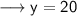
Hence ,

• No. of 2 point question = 30
• No. of 5 point question = 20