Answer:
See Below.
Explanation:
We want to prove the trigonometric identity:
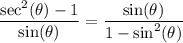
To start, let's simplify the right side. Recall the Pythagorean Identity:
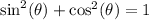
Therefore:
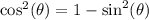
Substitute:
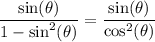
Split:
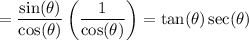
Therefore, our equation becomes:

From the Pythagorean Identity, we can divide both sides by cos²(θ). This yields:
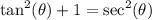
So:
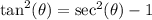
Substitute:
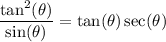
Rewrite:
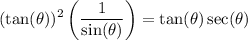
Recall that tan(θ) = sin(θ)/cos(θ). So:
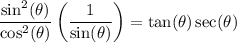
Simplify:

Simplify:
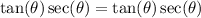
Hence proven.