Question

Consider a coaxial cable (like the kind that is used to carry a signal to your TV). In this cable, a current I runs in one direction along the inner central wire, and the same current I runs in the opposite direction in the hollow conductor. How does the magnetic field B outside the entire cable (outside both the inner wire as well as the hollow conductor) vary as a function of distance away from the cable

Answer 1

The magnetic field outside a coaxial cable is zero, as the opposite currents in the inner wire and hollow conductor cancel each other out. The magnetic field strength is only non-zero in the region between the two conductors, as determined by Ampère's law.

Step-by-step explanation:

The magnetic field B outside a coaxial cable, where the currents in the inner wire and hollow conductor flow in opposite directions, can be analyzed using Ampère's law. This law implies that if we consider a circular path outside of the cable (where r is greater than the radius of the outer conductor), the net current enclosed by this path is zero because the current in the inner conductor is equal and opposite to that in the outer conductor. Therefore, the magnetic field outside the coaxial cable is zero.

If we apply Ampère's law to a path within the cable but outside the inner conductor, we find that the magnetic field is not zero in this region because a net current is enclosed by such a path. Ampère's law reveals that all magnetic energy is stored in the space between the two conductors, and thus the strength of the magnetic field only has a non-zero value in this area. In conclusion, there is no magnetic field outside the coaxial cable as the inner and outer currents cancel out, but there is a field between the conductors.

Answer 2

0 < r < r_exterior B_total =
`(\mu_o I)/(2\pi r)`

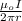
r > r_exterior B_total = 0

Step-by-step explanation:

The magnetic field created by the wire can be found using Ampere's law

∫ B. ds = μ₀ I

bold indicates vectors and the current is inside the selected path

outside the inner cable

B₁ (2π r) = μ₀ I

B₁ =
`(\mu_o I)/(2\pi r)`

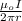
the direction of this field is found by placing the thumb in the direction of the current and the other fingers closed the direction of the magnetic field which is circular in this case.

For the outer shell

for the case r> r_exterior

B₂ = \frac{\mu_o I}{2\pi r}

This current is in the opposite direction to the current in wire 1, so the magnetic field has a rotation in the opposite direction

for the case r <r_exterior

in this case all the current is outside the point of interest, consequently not as there is no internal current, the field produced is zero

B₂ = 0

Now we can find the field created by each part

0 < r < r_exterior

B_total = B₁

B_total =
`(\mu_o I)/(2\pi r)`

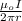
r > r_exterior

B_total = B₁ -B₂

B_total = 0