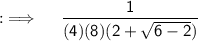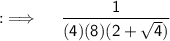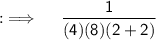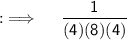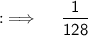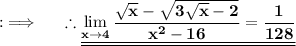Question

Evaluate the limit


`\rm\displaystyle\lim_(\rm x\to 4)\left(\frac{√(\rm x)-\sqrt{3√(\rm x)-2}}{\rm x^2-16}\right)=\ldots` ​

Answer 1

We can transform the limand into a proper rational expression by substitution.

Let y = √x. Then as x approaches 4, y will approach √4 = 2. So

`\displaystyle \lim_(x\to4)(\sqrt x - √(3 \sqrt x - 2))/(x^2 - 16) = \lim_(y\to2) (y - √(3y-2))/(y^4 - 16)`

Now let z = √(3y - 2). Then as y approaches 2, z will approach √(3•2 - 2) = 2 as well. It follows that y = (z² + 2)/3, so that

`\displaystyle \lim_(y\to2) (y - √(3y-2))/(y^4-16) = \lim_(z\to2) \frac{\frac{z^2+2}3 - z}{((z^2+2)^4)/(81)-16} \\\\ = \lim_(z\to2) (27(z^2+2)-81z)/((z^2+2)^4 - 1296) \\\\ = 27 \lim_(z\to2) (z^2 - 3z + 2)/(z^8 + 8z^6 + 24z^4 + 32z^2 - 1280)`

Plugging z = 2 into the denominator returns a value of 0, which means z - 2 divides z⁸ + 8z⁶ + 24z⁴ + 32z² - 1280 exactly. Polynomial division shows that

`(z^8 + 8z^6 + 24z^4 + 32z^2 - 1280)/(z-2) \\\\ = z^7+2z^6+12z^5+24z^4+72z^3+144z^2+320z+640`

and it's easy to see that the numerator is also divisible by z - 2, since

`z^2 - 3z + 2 = (z - 1) (z - 2)`

So, we can eliminate the factor of z - 2 and we're left with

`\displaystyle 27 \lim_(z\to2) (z^2 - 3z + 2)/(z^8 + 8z^6 + 24z^4 + 32z^2 - 1280) = 27 \lim_(z\to2)(z-1)/(z^7+\cdots+640)`

The remaining limand is continuous at z = 2, so we can evaluate the limit by direct substitution:

`\displaystyle 27 \lim_(z\to2)(z-1)/(z^7+\cdots+640) = (27)/(3456) = \boxed{\frac1{128}}`

Answer 2

We are given with a limit and we need to find it's value so let's start !!!!

`{\quad \qquad \blacktriangleright \blacktriangleright \displaystyle \sf \lim_(x\to 4)\frac{√(x)-\sqrt{3√(x)-2}}{x^(2)-16}}`

But , before starting , let's recall an identity which is the main key to answer this question

• 
  `{\boxed{\bf{a^(2)-b^(2)=(a+b)(a-b)}}}`

Consider The limit ;

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{√(x)-\sqrt{3√(x)-2}}{x^(2)-16}}`

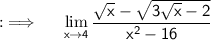
Now as directly putting the limit will lead to indeterminate form 0/0. So , Rationalizing the numerator i.e multiplying both numerator and denominator by the conjugate of numerator

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{√(x)-\sqrt{3√(x)-2}}{x^(2)-16}* \frac{√(x)+\sqrt{3√(x)-2}}{√(x)+\sqrt{3√(x)-2}}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-\sqrt{3√(x)-2})(√(x)+\sqrt{3√(x)-2})}{(x^(2)-4^(2))(√(x)+\sqrt{3√(x)-2})}}`

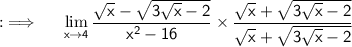
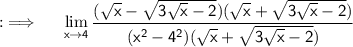
Using the above algebraic identity ;

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x))^(2)-(\sqrt{3√(x)-2})^(2)}{(x-4)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{x-(3√(x)-2)}{(x-4)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{x-3√(x)+2}{\{(√(x))^(2)-2^(2)\}(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{x-3√(x)-2}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

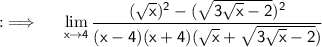
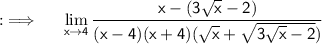
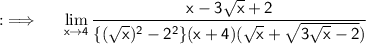
Now , here we need to eliminate (√x-2) from the denominator somehow , or the limit will again be indeterminate ,so if you think carefully as I thought after seeing the question i.e what if we add 4 and subtract 4 in numerator ? So let's try !

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{x-3√(x)-2+4-4}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(x-4)+2+4-3√(x)}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

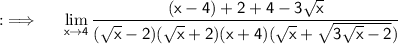
Now , using the same above identity ;

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-2)(√(x)+2)+6-3√(x)}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-2)(√(x)+2)+3(2-√(x))}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

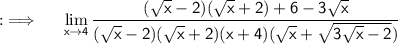
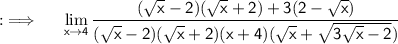
Now , take minus sign common in numerator from 2nd term , so that we can take (√x-2) common from both terms

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-2)(√(x)+2)-3(√(x)-2)}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

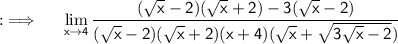
Now , take (√x-2) common in numerator ;

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-2)\{(√(x)+2)-3\}}{(√(x)-2)(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

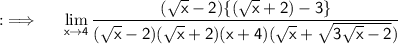
Cancelling the radical that makes our limit again and again indeterminate ;

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{\cancel{(√(x)-2)}\{(√(x)+2)-3\}}{\cancel{(√(x)-2)}(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)+2-3)}{(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

`{:\implies \quad \displaystyle \sf \lim_(x\to 4)\frac{(√(x)-1)}{(√(x)+2)(x+4)(√(x)+\sqrt{3√(x)-2})}}`

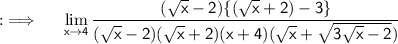
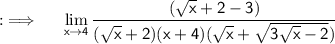
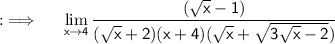
Now , putting the limit ;

`{:\implies \quad \sf \frac{√(4)-1}{(√(4)+2)(4+4)(√(4)+\sqrt{3√(4)-2})}}`

`{:\implies \quad \sf (2-1)/((2+2)(4+4)(2+√(3* 2-2)))}`

`{:\implies \quad \sf (1)/((4)(8)(2+√(6-2)))}`

`{:\implies \quad \sf (1)/((4)(8)(2+√(4)))}`

`{:\implies \quad \sf (1)/((4)(8)(2+2))}`

`{:\implies \quad \sf (1)/((4)(8)(4))}`

`{:\implies \quad \sf (1)/(128)}`

`{:\implies \quad \bf \therefore \underline{\underline{\displaystyle \bf \lim_(x\to 4)\frac{√(x)-\sqrt{3√(x)-2}}{x^(2)-16}=(1)/(128)}}}`