Answer:
The value of x is 6 .
Step-by-step explanation:
Solution :
Here's the required formula of median of trapezoid :
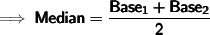
Where :
- ➝ Median
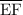 = 15
= 15 - ➝ Base₁ (AB) = x + 1
- ➝ Base₂ (CD) = 3x + 5
Substituting all the given values in the formula to find the value of x :
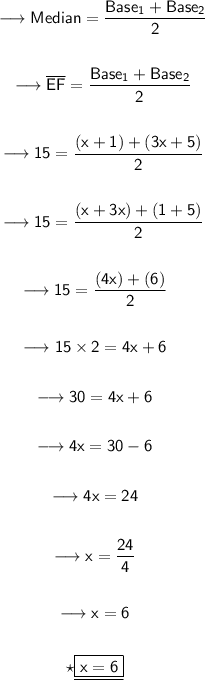
Hence, the value of x is 6.
