Answer:
i. The ratio of the areas of the two triangles is 5:8.
ii. The area of the larger triangle is 24 in².
Explanation:
Let the area of the smaller triangle be represented by
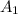 , and that of the larger triangle by
, and that of the larger triangle by
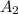 .
.
Area of a triangle =
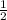 x b x h
x b x h
Where; b is its base and h the height.
Thus,
a. The ratio of the area of the two triangles is:
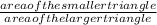
Area of smaller triangle =
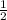 x b x h
x b x h
=
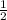 x 5 x h
x 5 x h
=
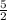 h
h
Area of the lager triangle =
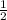 x b x h
x b x h
=
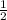 x 8 x h
x 8 x h
= 4h
So that;
Ratio =
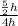
=
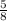
The ratio of the areas of the two triangles is 5:8.
b. If the area of the smaller triangle is 15 in², then the area of the larger triangle can be determined as;
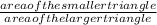 =
=
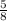
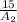 =
=
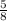
5
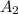 = 15 x 8
= 15 x 8
= 120
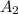 =
=
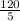
= 24
The area of the larger triangle is 24 in².