Question

Two triangles have bases with lengths 5in and 8in.

a. Find the ratio of the areas of the triangles

b. If the area of the smaller triangle is 15in², what is the area of the larger triangle?

Show work ​

Answer 1

i. The ratio of the areas of the two triangles is 5:8.

ii. The area of the larger triangle is 24 in².

Explanation:

Let the area of the smaller triangle be represented by
`A_(1)`, and that of the larger triangle by
`A_(2)`.

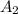Area of a triangle =
`(1)/(2)` x b x h

Where; b is its base and h the height.

Thus,

a. The ratio of the area of the two triangles is:

`(area of the smaller triangle)/(area of the larger triangle)`

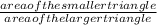
Area of smaller triangle =
`(1)/(2)` x b x h

=
`(1)/(2)` x 5 x h

=
`(5)/(2)`h

Area of the lager triangle =
`(1)/(2)` x b x h

=
`(1)/(2)` x 8 x h

= 4h

So that;

Ratio =
`((5)/(2)h )/(4h)`

=
`(5)/(8)`

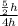
The ratio of the areas of the two triangles is 5:8.

b. If the area of the smaller triangle is 15 in², then the area of the larger triangle can be determined as;

`(area of the smaller triangle)/(area of the larger triangle)` =
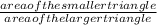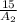`(5)/(8)`

`(15)/(A_(2) )` =
`(5)/(8)`

5
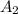`A_(2)` = 15 x 8

= 120

`A_(2)` =
`(120)/(5)`

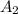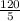
= 24

The area of the larger triangle is 24 in².