Question

The function ggg models the number of mosquitoes (in millions of mosquitoes) in a certain area as a function of rainfall (in centimeters) in that area.

Answer 1

6cm produces the largest mosquito

Explanation:

The question has missing details.

From the complete question, the function is:

`g(x) = 12x-x^2`

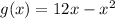
Required

Which area of rainfall produces the most mosquito

This implies that, we calculate the maximum of the function.

This is calculated as:

`Max = -(b)/(2a)`

We have:

`g(x) = 12x-x^2`

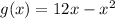
Rewrite as:

`g(x) = -x^2 + 12x + 0`

From the above:

`a= -1`

`b = 12`

`c = 0`

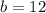
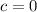
So, we have:

`Max = -(b)/(2a)`

`Max = -(12)/(2 * -1)`

`Max = (12)/(2)`

`Max = 6`

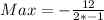
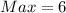
This implies that:

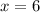`x = 6` ---- the maximum

When rainfall is at 6cm, there is a maximum number of mosquitoes

The maximum is then calculated as:

`g(x) = 12x-x^2`

`g(6) = 12 * 6 - 6^2`

`g(6) = 72 - 36`

`g(6) = 36`

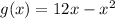
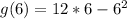
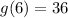
The maximum number of mosquito is 36 million