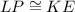1 Answer

PiersyP · Answer 1 · 2022-08-06T05:13:14+0000

Answer:

See Below.

Explanation:

We are given that:

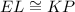
$EL\cong KP$

And we want to prove that:

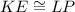
$KE\cong LP$

Congruent chords have congruent arcs. Therefore:

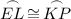
$\stackrel{\frown}{EL}\, \cong \, \stackrel{\frown}{KP}$

Arc EL is the sum of Arcs LP and PE:

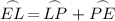
$\stackrel{\frown}{EL}\,=\, \stackrel{\frown}{LP}+\stackrel{\frown}{PE}$

Likewise, Arc KP is the sum of Arcs KE and PE:

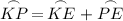
$\stackrel{\frown}{KP}\, =\, \stackrel{\frown}{KE}+\stackrel{\frown}{PE}$

Since Arcs EL and KP are congruent:

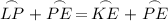
$\stackrel{\frown}{LP}+\stackrel{\frown}{PE}\, =\, \stackrel{\frown}{KE}+\stackrel{\frown}{PE}$

Subtraction Property of Equality:

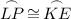
$\stackrel{\frown}{LP} \, \cong\, \stackrel{\frown}{KE}$

Congruent arcs have congruent chords. Therefore:

$LP\cong KE$

Please log in or register to add a comment.