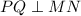Question

`\bigstar \: \underline{ \underline{ \tt{Question}}} :` In the given figure , M and N are the centres of two intersecting circles. Prove that :

i. PQ
`\perp` MN
ii. PR = RQ

~Thanks in advance! <3

Answer 1

Explanation:

First step is to prove triangle MPN ad MQN are congruent.

MP=MQ, radius of circle M

NP=NQ, radius of circle N

we have two S in SAS and for A, we need to prove angle MPN = MQN

consider triangle QMP, it is isosceles so angle MPQ = MQP

consider triangle QNP; it is isosceles so angle QPN = PQN

combining the two above

angle MPN = MPQ+QPN = MQP+PQN = MQN

By SAS, triangle MPN and MQN are congruent

By symmetry, MN is perpendicular to PQ

It also disects PQ so PR = RQ

Answer 2

See Below.

Explanation:

We are given two intersecting circles with centers M and N.

And we want to prove that: I) PQ ⊥ MN and that II) PR = RQ.

Since MP and MQ are radii of the same circle:

`MP\cong MQ`

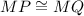
Likewise, since NP and NQ are radii of the same circle:

`NP\cong NQ`

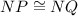
And by the Reflexive Property:

`PQ\cong PQ`

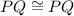
Therefore, by SSS Congruence:

`\Delta MPN\cong \Delta MQN`

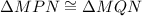
By CPCTC:

`\displaystyle \angle PMN\cong \angle QMN`

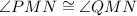
And by the Reflexive Property:

`MR\cong MR`

And since they are the radii of the same circle:

`MP\cong MQ`

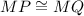
Therefore, by SAS Congruence:

`\Delta MPR\cong \Delta MQR`

Therefore, by CPCTC:

`PR\cong RQ`

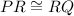
Note that PQ is a chord in Circle M.

Therefore:

`\text{Segment $MN$ bisects chord $PQ$}`

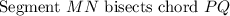
In a circle, a segment that passes through the center of the circle that is perpendicular to a chord also bisects the chord.

And conversely, a segment that passes through the center of a circle that bisects a chord in the circle is also perpendicular to the chord.

So:

`\displaystyle PQ\perp MN`