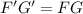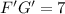Question

Segment FG begins at point F(-2, 4) and ends at point G(-2, -3). The segment is translated 3 units left and 2 units up, then reflected across the y-axis to form segment F'G'.How many units long is segment F'G'?

Answer 1

`F'G' = 7`

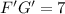
Explanation:

Given

`F = (-2,4)`

`G = (-2,-3)`

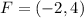
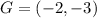
Required

Distance of F'G'

The transformation that give rise to F'G' from FG are:

• Translation
• Reflection

The above transformations are referred to as rigid transformation, and as such the side lengths remain unchanged.

i.e.

`F'G' = FG`

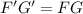
Calculating FG, we have:

`FG = √((x_1 - x_2)^2 + (y_1 - y_2)^2)`

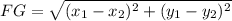
Where:

`F = (-2,4)` ---
`(x_1,y_1)`

`G = (-2,-3)` ---
`(x_2,y_2)`

`FG = √((-2 - -2)^2 + (4 - -3)^2)`

`FG = √((0)^2 + (7)^2)`

`FG = √(0 + 49)`

`FG = √(49)`

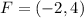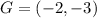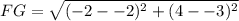
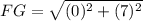
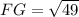
Take positive square root

`FG = 7`

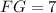
Recall that:

`F'G' = FG`

`F'G' = 7`