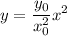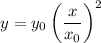Question

Marine biologists have determined that when a shark detectsthe presence of blood in the water, it will swim in the directionin which the concentration of the blood increases mostrapidly. Based on certain tests in seawater, theconcentration of blood(in parts per million) at point P(x,y) on thesurface is approximated by:

C(x,y)= e^- (x^2+2y^2).10^4

where x and y are measured in meters in a rectangularcoordinate system with the blood source at the origin.
a. Identify the level curves of the concentration function andsketch several members of this family together with a path that ashark will follow to the source.
b. Suppose a shark is at the point (xo, yo) when it first detects the presenceof blood in the water. Find an equation of the shark's path bysetting up and solving a differential equation.

Answer 1

a). The level curves of the function :

`$C(x,y) = e^(-(x^2+2y^2)/10^4)$`

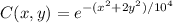
are actually the curves

`$e^(-(x^2+2y^2)/10^4)=k$`

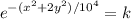
where k is a positive constant.

The equation is equivalent to

`$x^2+2y^2=K$`

`$\Rightarrow (x^2)/((\sqrt K)^2)+\frac{y^2}{(\sqrt {K/2})^2}=1, \text{ where}\ K = -10^4 \ln k$`

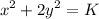
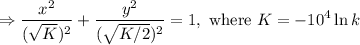
which is a family of ellipses.

We sketch the level curves for K =1,2,3 and 4.

If the shark always swim in the direction of maximum increase of blood concentration, its direction at any point would coincide with the gradient vector.

Then we know the shark's path is perpendicular to the level curves it intersects.

b). We have :

`$\triangledown C= (\partial C)/(\partial x)i+(\partial C)/(\partial y)j$`

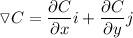
`$\Rightarrow \triangledown C =-(2)/(10^4)e^(-(x^2+2y^2)/10^4)(xi+2yj),$` and

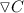`$\triangledown C$` points in the direction of most rapid increase in concentration, which means
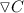`$\triangledown C$` is tangent to the most rapid increase curve.

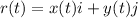`$r(t)=x(t)i+y(t)j$` is a parametrization of the most
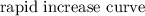`$\text{rapid increase curve}$` , then

`$(dx)/(dt)=(dx)/(dt)i+(dy)/(dt)j$` is a tangent to the curve.

So then we have that
`$(dr)/(dt)=\lambda \triangledown C$`

`$\Rightarrow (dx)/(dt)=-(2\lambda x)/(10^4)e^(-(x^2+2y^2)/10^4), (dy)/(dt)=-(4\lambda y)/(10^4)e^(-(x^2+2y^2)/10^4) $`

∴
`$(dy)/(dx)=(dy/dt)/(dx/dt)=(2y)/(x)$`

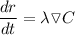
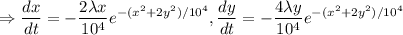
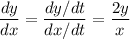
Using separation of variables,

`$(dy)/(y)=2(dx)/(x)$`

`$\int(dy)/(y)=2\int (dx)/(x)$`

`$\ln y=2 \ln x$`

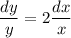
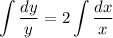
⇒ y = kx^2 for some constant k

but we know that
`$y(x_0)=y_0$`

`$\Rightarrow kx_0^2=y_0$`

`$\Rightarrow k =(y_0)/(x_0^2)$`

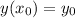
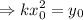
∴ The path of the shark will follow is along the parabola

`$y=(y_0)/(x_0^2)x^2$`

`$y=y_0\left((x)/(x_0)\right)^2$`