Question

A relaxed biceps muscle requires a force of 25.4 N for an elongation of 3.20 cm; under maximum tension, the same muscle requires a force of 520 N for the same elongation. Find Young's modulus (Pa) for the muscle tissue under each of these conditions if the muscle can be modeled as a uniform cylinder with an initial length of 0.200 m and a cross-sectional area of 50.0 cm2.

Answer 1

Y = 31750 Pa = 31.75 KPa (For 24.5 N force)

Y = 312500 Pa = 312.5 KPa (For 250 N force)

Step-by-step explanation:

Since the elongation is constant. Therefore, the strain will remain the same in both cases:

`Strain = (Elongation)/(Original\ Length)\\\\Strain = (0.032\ m)/(0.2\ m)\\\\Strain = 0.16`

FOR A FORCE OF 25.4 N:

`Stress = (Force)/(Area)\\\\Stress = (25.4\ N)/(0.005\ m^2)\\\\Sress = 5080\ Pa = 5.08\ KPa`

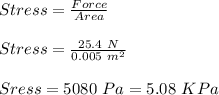
Now, for Young's Modulus:

`Y = (Stress)/(Strain)\\\\Y = (5080\ Pa)/(0.16)`

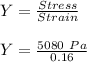
Y = 31750 Pa = 31.75 KPa

FOR A FORCE OF 520 N:

`Stress = (Force)/(Area)\\\\Stress = (250\ N)/(0.005\ m^2)\\\\Sress = 50000\ Pa = 50\ KPa`

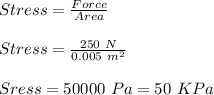
Now, for Young's Modulus:

`Y = (Stress)/(Strain)\\\\Y = (50000\ Pa)/(0.16)`

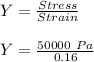
Y = 312500 Pa = 312.5 KPa