Answer:
95% confidence interval for the population is; -0.9525 <
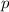 < -0.9505
< -0.9505
Explanation:
Given the data in the question;
correlation coefficient y between output and time under a load of 588 N was −0.9515
so first we determine the quantity W.
we know that; W =
 ln(
ln(
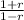 )
)
we substitute -0.9515 for r
W =
 ln(
ln(
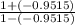 )
)
W =
 ln(
ln(
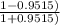 )
)
W =
 ln(
ln(
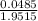 )
)
W =
 ln( 0.02485 )
ln( 0.02485 )
W =
 ( -3.6948975 )
( -3.6948975 )
W = - 1.8474
So the quantity W is normally distributed with standard deviation given by;
σ
 = 1 / √(n - 3)
= 1 / √(n - 3)
given that n is 33,000, we substitute
σ
 = 1 / √(33,000 - 3)
= 1 / √(33,000 - 3)
σ
 = 1 / √32997
= 1 / √32997
σ
 = 0.0055
= 0.0055
Now, at 95% confidence interval, μ
 will be;
will be;
⇒ - 1.8474 - 1.96( 0.0055 ) < μ
 < - 1.8474 + 1.96( 0.0055 )
< - 1.8474 + 1.96( 0.0055 )
⇒ - 1.8474 - 0.01078 < μ
 < - 1.8474 + 0.01078
< - 1.8474 + 0.01078
⇒ -1.8582 < μ
 < -1.8366
< -1.8366
So to obtain 95% confidence interval for p, we use the following equation;
we transform the inequality
p = [(
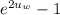 ) / (
) / (
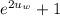 )]
)]
we substitute
 <
<
 <
<
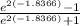
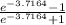 <
<
 <
<
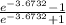
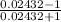 <
<
 <
<
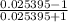
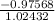 <
<
 <
<
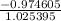
-0.9525 <
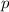 < -0.9505
< -0.9505
Therefore, 95% confidence interval for the population is; -0.9525 <
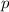 < -0.9505
< -0.9505