Question

Suppose a 65 kg person stands at the edge of a 6.5 m diameter merry-go-round turntable that is mounted on frictionless bearings and has a moment of inertia of 1850 kgm2. The turntable is at rest initially, but when the person begins running at a speed of 3.8 m/s (with respect to the turntable) around its edge, the turntable begins to rotate in the opposite direction. Calculate the angular velocity of the turntable. (Hint: use what you know about relative velocity to help solve the problem

Answer 1

`0.3165\ \text{rad/s}`

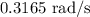
Step-by-step explanation:

m = Mass of person = 65 kg

d = Diameter of round table = 6.5 m

r = Radius =
`(d)/(2)=3.25\ \text{m}`

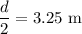
v = Velocity of person running = 3.8 m/s

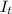`I_t` = Moment of inertia of turntable =
`1850\ \text{kg m}^2`

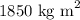
Moment of inertia of the system is

`I=I_t+mr^2\\\Rightarrow I=1850+65* 3.25^2\\\Rightarrow I=2536.5625\ \text{kg m}^2`

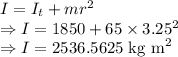
As the angular momentum of the system is conserved we have

`L_i=L_f\\\Rightarrow mvr=I\omega_f\\\Rightarrow \omega_f=(mvr)/(I)\\\Rightarrow \omega_f=(65* 3.8* 3.25)/(2536.5625)\\\Rightarrow \omega_f=0.3165\ \text{rad/s}`

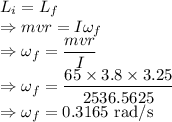
The angular velocity of the turntable is
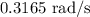`0.3165\ \text{rad/s}`.