Answer:
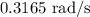
Step-by-step explanation:
m = Mass of person = 65 kg
d = Diameter of round table = 6.5 m
r = Radius =

v = Velocity of person running = 3.8 m/s
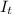 = Moment of inertia of turntable =
= Moment of inertia of turntable =

Moment of inertia of the system is

As the angular momentum of the system is conserved we have
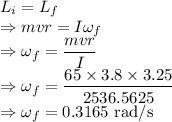
The angular velocity of the turntable is
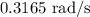 .
.