Answer:
the surface temperature of the plates when they come out of the oven is approximately 445 °C
Step-by-step explanation:
Given the data in the question;
thickness t = 3 cm = 0.03 m
so half of the thickness L = 0.015 m
thermal conductivity of brass k = 110 W/m°C
Density p = 8530 kg/m³
specific heat
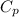 = 380 J/kg°C
= 380 J/kg°C
thermal diffusivity of brass ∝ = 33.9 × 10⁻⁶ m²/s
Temperature of oven T₀₀ = 700°C
initial temperature T
 = 25°C
= 25°C
time t = 10 min = 600 s
convection heat transfer coefficient h = 80 W/m².K
Since the plate is large compared to its thickness, the heat conduction is one dimensional. heat transfer coefficient and thermal properties are constant over the entire surface.
So, using analytical one-term approximation method, the Fourier number > 0.2.
now, we determine the Biot number for the process
we know that; Biot number Bi = hL / k
so we substitute
Bi = hL / k
Bi = (80 × 0.015) / 110 = 1.2 / 110 = 0.0109
Now, we get the constants λ₁ and A₁ corresponding to Biot Number ( 0.0109 )
The interpolation method used to find the
λ₁ = 0.1039 and A₁ = 1.0018
so
The Fourier number т = ∝t/L²
we substitute
Fourier number т = ( (33.9 × 10⁻⁶)(600) ) / (0.015)²
т = 0.02034 / 0.000225
т = 90.4
As we can see; 90.4 > 0.2
So, analytical one-term approximation can be used.
∴ Temperature at the surface will be;
θ(L,t)
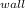 = (T(x,t) - T₀₀) / (T
= (T(x,t) - T₀₀) / (T
 - T₀₀) ----- let this be equation
- T₀₀) ----- let this be equation
θ(L,t)
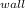 = [A₁e^(-λ₁²т)]cos( λ₁L / L )
= [A₁e^(-λ₁²т)]cos( λ₁L / L )
so we substitute
θ(L,t)
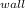 = [1.0018e^(- (0.1039)²× 90.4 )] cos( 0.1039 × 0.015 / 0.015 )
= [1.0018e^(- (0.1039)²× 90.4 )] cos( 0.1039 × 0.015 / 0.015 )
θ(L,t)
 = [1.0018e^(- 0.975886984 )] cos( 0.1039 )
= [1.0018e^(- 0.975886984 )] cos( 0.1039 )
θ(L,t)
 = [1.0018 × 0.376857938] × 0.999998
= [1.0018 × 0.376857938] × 0.999998
θ(L,t)
 = 0.3775
= 0.3775
so we substitute into equation 1
θ(L,t)
 = (T(L,t) - T₀₀) / (T
= (T(L,t) - T₀₀) / (T
 - T₀₀)
- T₀₀)
0.3775 = ( T(L,t) - 700 ) / ( 25 - 700 )
0.3775 = ( T(L,t) - 700 ) / ( - 675 )
0.3775 × ( - 675 ) = ( T(L,t) - 700 )
- 254.8125 = T(L,t) - 700
T(L,t) = 700 - 254.8125
T(L,t) = 445.1875 °C ≈ 445 °C
Therefore, the surface temperature of the plates when they come out of the oven is approximately 445 °C