Answer:
the ratio of her final kinetic energy to her initial kinetic energy is 1.7.
Step-by-step explanation:
Given;
initial angular speed, ω₁ = 5.9 rad/s
let her initial moment of inertia = I₁
her final moment of inertia

Apply the principle of conservation of angular momentum to determine the final angular speed of the girl;
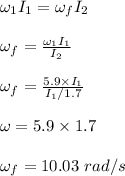
The initial rotational kinetic energy is given as;
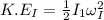
The final rotational kinetic energy is given as;

The ratio of her final kinetic energy to her initial kinetic energy is given as;
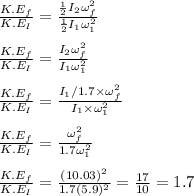
Therefore, the ratio of her final kinetic energy to her initial kinetic energy is 1.7.