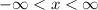Answer:
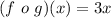
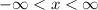
Explanation:
Given
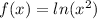
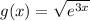
Solving (a): (f o g)(x)
This is calculated as:
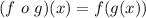
We have:
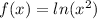
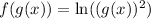
Substitute:
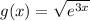
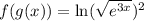
Evaluate the square
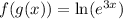
Using laws of natural logarithm:
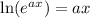
So:
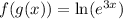
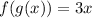
Hence:
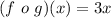
Solving (b): The domain
We have:
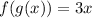
The above function has does not have any undefined points and domain constraints.
Hence, the domain is: