Question

The product of two rational numbers is irrational.

Answer 1

The statement is false.

Explanation:

Here we need to remember some things:

Integer numbers are closed under multiplication.

This means that for two integers a and b, the product a*b is also an integer.

A rational number is a number that can be written as the quotient of two integer numbers.

An irrational number is a number that can't be written as the quotient of two rational numbers.

Now let's see the statement:

"The product of two rational numbers is irrational."

The product of two rational numbers is written as:

`(a)/(b) *(c)/(d)`

Where a, c, b, and d are integers.

We can rewrite that product as:

`(a*c)/(b*d)`

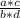
Because of the first property, we know that a*c is an integer, and b*d is also an integer, so here we have a quotient of two integer numbers, so this is a rational number.

Then the product of two rational numbers is a rational number.

Then the statement is false.