Answer:
The statement is false.
Explanation:
Here we need to remember some things:
Integer numbers are closed under multiplication.
This means that for two integers a and b, the product a*b is also an integer.
A rational number is a number that can be written as the quotient of two integer numbers.
An irrational number is a number that can't be written as the quotient of two rational numbers.
Now let's see the statement:
"The product of two rational numbers is irrational."
The product of two rational numbers is written as:

Where a, c, b, and d are integers.
We can rewrite that product as:
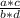
Because of the first property, we know that a*c is an integer, and b*d is also an integer, so here we have a quotient of two integer numbers, so this is a rational number.
Then the product of two rational numbers is a rational number.
Then the statement is false.