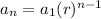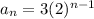Answer:
Explicit :
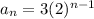
Recursive: a₁ = 1
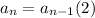
Explanation:
We have to write the recursive formula for the geometric sequence with second term 2 and third term 12.
Geometric sequence will be in the form of,
a, ar, ar², ar³,...........
Here, r = common ratio
a = first term of the sequence
Here, ar = 6 ------(1)
And ar² = 12 ------(2)
By dividing equation (2) by (1),
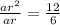
r = 2
From equation (1),
a(2) = 6
a = 3
Recursive formula of a geometric sequence is given by,
a₁ = a

Therefore, for the given sequence,
a₁ = 1
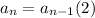
Similarly, explicit formula of the geometric sequence is given by,