Answer:
Given that the manufacturers claim is true, the probability that the sample mean area is 249.6 ft.² or less is 0.42074
Explanation:
The manufacturer claims that mean amount of foil on each roll, μ = 250 ft²
The standard deviation of the measured amount of foil per roll, σ = 2 ft.²
The number of rolls tested by the restaurant, n = 10 rolls
The mean measured by the restaurant,
 = 249.6
= 249.6
Taking the sample means as individual score, we have;
The z-score, of the sample mean is given as follows;
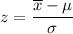
At
 = 249.6, we have;
= 249.6, we have;
z = (249.6 - 250)/2 = -0.2
Therefore, the probability for a mean less than or equal to 249.6, we have;
The probability, P = P(z < -0.2) = 0.42074
The probability that the sample mean area is 249.6 ft.² or less given that the manufacturers claim is true, P = 0.42074.