Question

If JK is tangent to circle L, find x​

Answer 1

if JK is tangent that means it creates 90° with X that is the ray of the circonference.

to find X first you have to find L and to do so you use the inverse of pythagorean theorem cause you have the hypotenouse :

sqr( 25^2-1^2) = 24.97

now divide by 2 and you have 12.49

Answer 2

Since JK is tangent to circle L, the value of x is equal to 24 units.

In Mathematics and Geometry, Pythagorean theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:

`c^2=a^2+b^2`

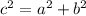
Where:

• a is the opposite side of a right-angled triangle.
• b is the adjacent side of a right-angled triangle.
• c is the hypotenuse of a right-angled triangle.

In order to determine the length of JM or the value of x, we would have to apply Pythagorean's theorem as follows;

`JM^2 = KM^2 - JK^2\\\\JM^2 = 25^2 - 7^2\\\\JM^2 = 625 - 49\\\\JM=√(576)`

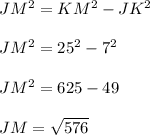
JM = x = 24 units.