Question

Help a formula word problem. Thank you if you help. You're a genuis!​

Answer 1

Answer: Choice (3) 28

==========================================================

Step-by-step explanation:

We start with one block at the very left side. This is algebraically written as
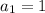`a_1 = 1`. The small subscript '1' means we're dealing with the first term, and that is set equal to 1. In other words, the first term is 1.

The second term is three since we have three blocks as the next figure down the line. So
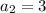`a_2 = 3`. We can then see that
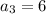`a_3 = 6` and
`a_4 = 10`

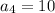
The sequence of the first four terms are: 1, 3, 6, 10.

The notation
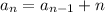`a_n = a_(n-1) + n` tells us "to get the nth term
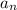`a_n`, we add the previous term (
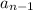`a_(n-1)`) to the value of n".

For example, if we wanted the third term, we would add the second term a2 onto the value of n = 2. In order to know a2, we need the diagram or you would have to use the recursive formula to find it.

Furthermore, it means that to find the fifth term
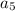`a_5`, we do the following

`a_n = a_(n-1) + n\\\\a_5 = a_(5-1) + 5\\\\a_5 = a_(4) + 5\\\\a_5 = 10+5\\\\a_5 = 15`

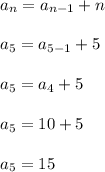
The fifth figure will have 15 small little blocks to it. You can draw this out by copying the fourth figure, and then adding 5 smaller blocks to the very bottom portion. The sixth figure is basically a copy of the fifth one, but we have six little blocks along the bottom. This is the "plus n" being applied in the recursive formula.

So the 6th figure will have 15+6 = 21 blocks in total while the 7th figure has 21+7 = 28 blocks. This points us to choice (3).

Side note: These are known as triangular numbers. Note how the gaps between consecutive values of 1,3,6,10,15,21,28 is +2,+3,+4,+5,+6,+7.