Question

What type of quadrilateral is quadrilateral ABCD if AB=4x-2, BC=2x+12, DC=3x+5, AD=6x-16, AC=4x+12, DB=8x-10, and x=7? Explain and use the properties of the types of quadrilaterals as proofs.

Answer 1

The quadrilateral ABCD is a square.

Explanation:

According to the statement, AB, BC, CD and DA are the sides of the quadrilateral, whereas DB and AC are its diagonals. If we know that
`x = 7`,
`AB = 4\cdot x - 2`,
`BC = 2\cdot x + 12`,
`DC = 3\cdot x +5`,
`AD = 6\cdot x -16`,
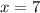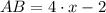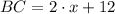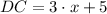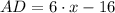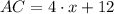`AC = 4\cdot x + 12` and
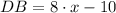`DB = 8\cdot x -10`, the lengths of each line segment are respectively:

Sides

`AB = 4\cdot (7) -2`

`AB = 26`

`BC = 2\cdot (7) +12`

`BC = 26`

`DC = 3\cdot (7) +5`

`DC = 26`

`AD = 6\cdot (7) -16`

`AD = 26`

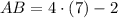
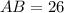
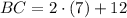
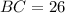
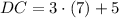
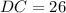
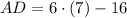
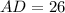
Diagonals

`AC = 4\cdot (7) +12`

`AC = 40`

`DB = 8\cdot (7) - 10`

`DB = 40`

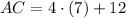
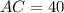
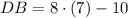
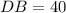
This information indicates that this quadrilateral is a square because of these characteristics:

1) All sides have the same length.

2) The ratio of any diagonal to any side is
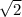`√(2)`.