Answer:
The quadrilateral ABCD is a square.
Explanation:
According to the statement, AB, BC, CD and DA are the sides of the quadrilateral, whereas DB and AC are its diagonals. If we know that
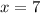 ,
,
 ,
,
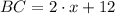 ,
,
 ,
,
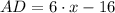 ,
,
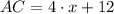 and
and
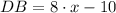 , the lengths of each line segment are respectively:
, the lengths of each line segment are respectively:
Sides


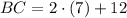
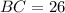
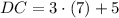
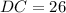
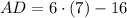
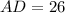
Diagonals

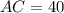
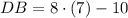

This information indicates that this quadrilateral is a square because of these characteristics:
1) All sides have the same length.
2) The ratio of any diagonal to any side is
 .
.