Answer:
Initial pop. = 1.8 (hundreds) = 180, 1 year, 1.2
Explanation:
The initial population is at time t = 0. Put 0 in for t to get
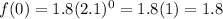 (measured in hundreds) so this population is 1.8(100) = 180
(measured in hundreds) so this population is 1.8(100) = 180
The time t is in years, so increasing t by 1 increases it by 1 year.
As t increases by 1, the factor that changes is 1.2 . For example,
At t = 2, the population is

At t = 3, the population is
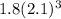
There is just one more factor of 2.1, so the population in year 3 is 2.1 times the population in year 2.