Question

Int sin(x+a)/sinx dx

Answer 1

`\displaystyle \rm x \cos(a) + \sin(a) \ln\left( | \sin(x) | \right) + C`

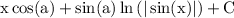
Explanation:

we would like to integrate the following integration:

`\displaystyle \int ( \sin(x + a) )/( \sin(x) ) dx`

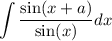
we can rewrite the denominator by using algebraic identity given by:

`\displaystyle \rm\sin( \alpha \pm \beta ) = \sin( \alpha ) \cos( \beta ) \pm \cos( \alpha ) \sin( \beta )`

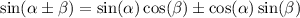
thus substitute:

`\displaystyle \int \frac{ \sin(x ) \cos(a) + \cos(x) \sin(a) } { \sin(x) } dx`

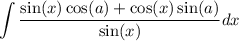
we should rewrite integrand as sum therefore we can use sum integration formula

`\displaystyle \rm\int \frac{ \sin(x ) \cos(a) } { \sin(x) } + \frac{ \cos(x) \sin( \alpha ) } { \sin(x) } dx`

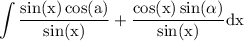
use sum integration formula:

`\displaystyle \rm\int \frac{ \sin(x ) \cos(a) } { \sin(x) } dx + \int \frac{ \cos(x) \sin( \alpha ) } { \sin(x) } dx`

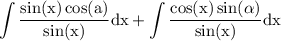
reduce fraction:

`\displaystyle \rm\int \cos(a) dx + \int \frac{ \cos(x) \sin( \alpha ) } { \sin(x) } dx`

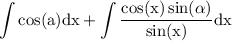
rewrite:

`\displaystyle \rm\int \cos(a) dx + \int \frac{ \cos(x) } { \sin(x) } \cdot \sin( a) dx`

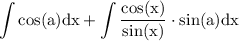
use trigonometric indentity:

`\displaystyle \rm\int \cos(a) dx + \int \cot(x) \cdot \sin( a) dx`

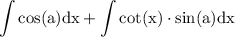
use constant integration formula

`\displaystyle \rm\int \cos(a) dx + \sin(a) \int \cot(x) dx`

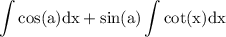
use integration rules:

`\displaystyle \rm x \cos(a) + \sin(a) \ln\left( | \sin(x) | \right)`

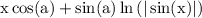
and finally we of course have to add constant of integration

`\displaystyle \rm x \cos(a) + \sin(a) \ln\left( | \sin(x) | \right) + C`

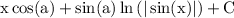
And we are done!

`\text{Note:I used integration by substitution to figure out }\\\displaystyle \int \cot(x)dx \:\text{part}`