Question

A toroidal solenoid has a radius of 0.12 m and a cross sectional area of 20×10^-4 m2. It is found that when the current is 20A, the energy is 0.1 J. How many turns does the winding have?

Answer 1

the number of turns in the winding is 387 turns.

Step-by-step explanation:

Given;

radius of the solenoid, r = 0.12 m

cross sectional area of the solenoid, A = 20 x 10⁻⁴ m²

current flowing through the solenoid, I = 20 A

the energy of the flowing current, E = 0.1 J

The energy stored in solenoid is given as;

`U = (1)/(2) LI^2\\\\L = (2U)/(I^2) \\\\L = (2 * 0.1)/(20^2) \\\\L = 5 * 10^(-4) \ H`

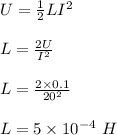
The number of turns in the winding is calculated as follows;

`L = (\mu_o N^2A)/(2\pi r) \\\\N^2 = (2\pi r L)/(\mu_o A) \\\\N = \sqrt{(2\pi r L)/(\mu_o A)} \\\\N = \sqrt{(2\pi * 0.12 * 5* 10^(-4) )/(4\pi * 10^(-7) * 20* 10^(-4) )}\\\\N = 387 \ turns`

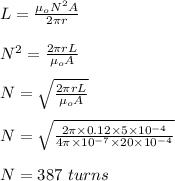
Therefore, the number of turns in the winding is 387 turns.