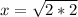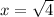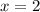Question

Solve the system.
9x2 + 4(y - 2)2 = 36
x² = 2y

Answer 1

`x =2`

`y =2`

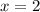
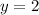
Explanation:

Given

`9x^2 + 4(y - 2)^2 = 36`

`x^2 = 2y`

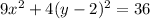
Required

Solve

Substitute:
`x^2 = 2y` in
`9x^2 + 4(y - 2)^2 = 36`

`9*2y + 4(y-2)^2 = 36`

`18y + 4(y-2)^2 = 36`

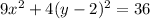
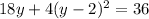
Open bracket

`18y + 4[y^2-2y - 2y + 4] = 36`

`18y + 4[y^2-4y + 4] = 36`

Open bracket

`18y + 4y^2-16y + 16 = 36`

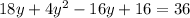
Collect like terms

`4y^2+18y-16y + 16 - 36 = 0`

`4y^2+2y-20= 0`

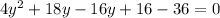
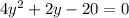
Divide through by 2

`2y^2+y-10= 0`

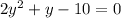
Expand

`2y^2+5y - 4y-10= 0`

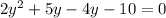
Factorize

`y(2y + 5) - 2(2y + 5) = 0`

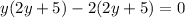
Factor out 2y + 5

`(y -2)(2y + 5) = 0`

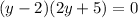
Split

`y - 2 =0\ or\ 2y + 5 = 0`

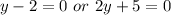
Solve for y

`y =2 \ or\y = -(5)/(2)`

We have:

`x^2 = 2y`

Make x the subject

`x = \sqrt{2y`

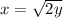
The above is true for positive y values.

So:
`y =2`

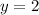
This gives

`x = \sqrt{2*2`

`x = \sqrt{4`

`x =2`