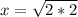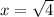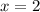Answer:
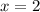
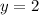
Explanation:
Given
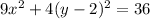

Required
Solve
Substitute:
 in
in
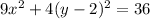
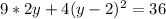
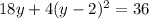
Open bracket
![18y + 4[y^2-2y - 2y + 4] = 36](https://img.qammunity.org/2022/formulas/mathematics/college/c74mlewdtu9fzzkvrf4yok23p307d0bv7h.png)
![18y + 4[y^2-4y + 4] = 36](https://img.qammunity.org/2022/formulas/mathematics/college/f4eyrcji11mpgrivkuuyax3e08woh13lo8.png)
Open bracket
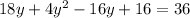
Collect like terms
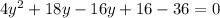
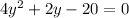
Divide through by 2
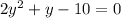
Expand
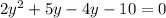
Factorize
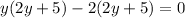
Factor out 2y + 5
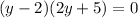
Split
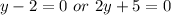
Solve for y
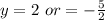
We have:

Make x the subject
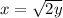
The above is true for positive y values.
So:
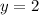
This gives