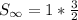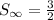Answer:
The sum of the series is 3/2
Explanation:
Given
1 + 1/3 + 1/3^2 + ....
Required
The sum of the series
This implies that we calculate the sum to infinity.
We have:
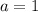 -- The first term
-- The first term
First, calculate the common ratio (r)
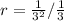
Change to product
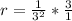
Solve
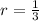
The sum of the series is then calculated as:
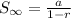
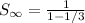
Solve the denominator
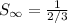
Express as product