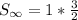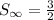Question

Sum of series 1 +1/3 +1/3².... is?​

Answer 1

The sum of the series is 3/2

Explanation:

Given

1 + 1/3 + 1/3^2 + ....

Required

The sum of the series

This implies that we calculate the sum to infinity.

We have:

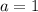`a = 1` -- The first term

First, calculate the common ratio (r)

`r = (1)/(3^2) / (1)/(3)`

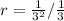
Change to product

`r = (1)/(3^2) * (3)/(1)`

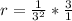
Solve

`r = (1)/(3)`

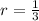
The sum of the series is then calculated as:

`S_(\infty) = (a)/(1 - r)`

`S_(\infty) = (1)/(1 - 1/3)`

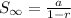
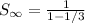
Solve the denominator

`S_(\infty) = (1)/(2/3)`

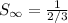
Express as product

`S_(\infty) = 1 * (3)/(2)`

`S_(\infty) = (3)/(2)`