Question

Triangle ABC has AB = 10 √3cm, AC=6cm and has area 45cm^2

(i) Find the size of angle CAB.

(ii) Find the length of BC

Answer 1

I) ∠CAB measures 60°.

II) BC measures approximately 15.23 cm.

*Please read notes.

Explanation:

We are given ΔABC, where AB measures 10√3 cm, AC measures 6 cm, and the triangle has an area of 45 square cm.

And we want to find I) the measure of ∠CAB and II) the length of BC.

I) First, we should always draw a representative triangle so we can determine the sides and angles. This is shown below.

Note that ∠CAB (or simply ∠A) is the angle between the two sides. Thus, we can find the angle by using the alternative formula for the area of a triangle:

`\displaystyle A=(1)/(2)ab\sin(C)`

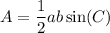
Where a and b are two side lengths, and C is the angle between the two sides.

Substitute:

`\displaystyle 45=(1)/(2)(10√(3))(6)\sin(A)`

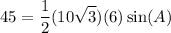
Simplify:

`\displaystyle 45=30√(3)\sin(A)`

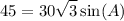
So:

`\displaystyle \sin(A)=(45)/(30√(3))=(3)/(2\sqrt3)=(√(3))/(2)`

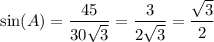
Take the inverse sine of both sides. Use a calculator. Thus:

`\displaystyle m\angle A=\sin^(-1)\left((√(3))/(2)\right)=60^\circ`

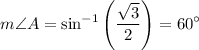
II) To find BC, we will use the Law of Cosines. We do not know whether or not ΔABC is a right triangle, so we cannot use right triangle trigonometry or special right triangles.

The law of cosines is:

`\displaystyle c^2=a^2+b^2-2ab\cos(C)`

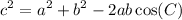
Where a and b are side lengths and C is the angle between the side lengths. c is the side length opposite to the angle.

BC is opposite to A. Substitute:

`(BC)^2=(10√(3))^2+(6)^2-2(10√(3))(6)\cos(60^\circ)`

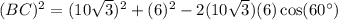
Simplify:

`\displaystyle BC^2=336-120√(3)\left((1)/(2)\right)=336-60√(3)`

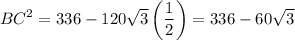
Take the square root of both sides:

`\displaystyle BC=\sqrt{336-60√(3)}\approx 15.23`

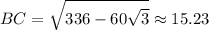
BC measures about 15.23 cm.

Notes:

In this case, the inverse sine of √3/2 will yield two answers: 60° and 120°. This is an example of an ambiguous case. Both of these angles will work. However, BC will be different. If ∠A is 60°, then BC is about 15.23. However, if ∠A is 120°, then BC is about 20.97. Both will result in the triangle having an area of 45 square cm, as well as AB measuring 10√3 and AC measuring 6.