Answer:
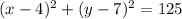
Explanation:
1) Find the radius
To find the radius of the circle, use the distance formula for the points (4,7) and (-7,9)
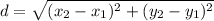 where the two points are
where the two points are
 and
and

Plug in the points (4,7) and (-7,9)
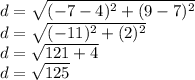
Therefore, the radius of the circle is
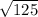 units.
units.
2) Plug all data into the circle equation
Equation of a circle (not centred at the origin):
 where the centre is
where the centre is
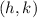
Plug in the point (4,7) as (h,k)
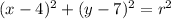
Plug in the radius
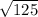
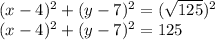
I hope this helps!