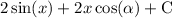Question

Help please!

integrate the following:

`\displaystyle \int ( \cos(2x) - \cos(2a) )/( \cos(x) - \cos( \alpha ) ) dx`
​

Answer 1

`\displaystyle 2 \sin(x) + 2x \cos( \alpha ) + \rm C`

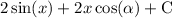
Explanation:

we would like to integrate the following integration:

`\displaystyle \int ( \cos(2x) - \cos(2 \alpha ) )/( \cos(x) - \cos( \alpha ) ) dx`

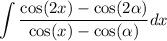
notice that you can simplify the integrand

recall that,

`\displaystyle \cos(2 \theta) = 2 \cos(\theta) ^(2) - 1`

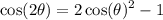
thus substitute:

`\displaystyle \int \frac{ 2\cos^(2) (x)- 1 - \{2\cos ^(2) (\alpha ) - 1 \} }{ \cos(x) - \cos( \alpha ) } dx`

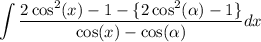
remove parentheses:

`\displaystyle \int ( 2\cos^(2) (x)- 1 - 2\cos ^(2) (\alpha ) + 1)/( \cos(x) - \cos( \alpha ) ) dx`

`\displaystyle \int ( 2\cos^(2) (x) - 2\cos ^(2) (\alpha ) )/( \cos(x) - \cos( \alpha ) ) dx`

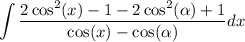
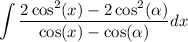
factor out 2:

`\displaystyle \int ( 2(\cos^(2) (x) - \cos ^(2) (\alpha )) )/( \cos(x) - \cos( \alpha ) ) dx`

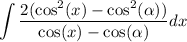
we can use algebraic identity i.e

a²-b²=(a+b)(a-b) to factor the denominator

`\displaystyle \int \frac{ 2(\cos^{} (x) + \cos ^{} (\alpha ))( \cos(x) - \cos( \alpha ) ) }{ \cos(x) - \cos( \alpha ) } dx`

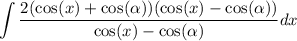
reduce fraction:

`\displaystyle \int \frac{ 2(\cos^{} (x) + \cos ^{} (\alpha ))( \cancel{\cos(x) - \cos( \alpha ) ) }}{ \cancel{\cos(x) - \cos( \alpha ) }} dx`

`\displaystyle \int 2( \cos(x) + \cos( \alpha ) )dx`

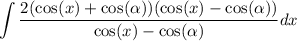
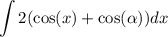
distribute:

`\displaystyle \int 2 \cos(x) + 2\cos( \alpha ) dx`

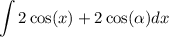
use sum integration formula:

`\rm \displaystyle \int 2 \cos(x) dx+ \int2\cos( \alpha ) dx`

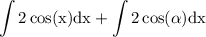
recall integration rules:

`\displaystyle 2 \sin(x) + 2x \cos( \alpha )`

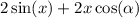
and we of course have to add constant of integration

`\displaystyle 2 \sin(x) + 2x \cos( \alpha ) + \rm C`