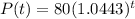Answer:
The hourly growth rate is of 4.43%.
The function showing the number of bacteria after t hours is
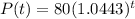
Explanation:
Equation of population growth:
The equation for the population after t hours is given by:
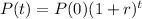
In which P(0) is the initial population and r is the growth rate, as a decimal.
The conditions are such that the number of bacteria is able to double every 16 hours.
This means that
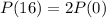 . We use this to find r.
. We use this to find r.
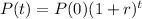
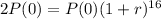
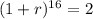
![\sqrt[16]{(1+r)^(16)} = \sqrt[16]{2}](https://img.qammunity.org/2022/formulas/mathematics/college/8l8fieu3h7eh16j32zfiwpqgr81uhigot1.png)
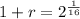
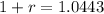
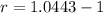
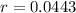
The hourly growth rate is of 4.43%.
80 bacteria are placed in a petri dish.
This means that
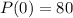 .
.
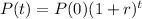
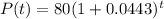
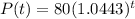
The function showing the number of bacteria after t hours is