Answer:
The 95% confidence interval for the population mean is
(79.2996, 81.9004)
Explanation:
Step(i):-
Given that the sample size 'n' = 168
Let 'X' be a Random variable in a normal distribution
Given that mean of the sample x⁻ = 80.60
Given that the standard deviation of the Population = 8.60
Step(ii):-
The 95% confidence interval for the population mean is determined by
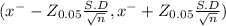

(80.60 -1.3004 , 80.60+1.3004)
(79.2996 , 81.9004)
Final answer:-
The 95% confidence interval for the population mean is
(79.2996, 81.9004)