Question

A 20 mm diameter rod made of ductile material with a yield strength of 350 MN/m2 is subjected to a torque of 100 N.m, and a bending moment of 150 N.m. An axial tensile force is then gradually applied. What is the value of the axial force when yielding of the rod occurs using: a. The maximum-shear-stress theory b. The maximum-distortional-energy theory.

Answer 1

a) 42.422 KN

b) 44.356 KN

Step-by-step explanation:

Given data :

Diameter = 20 mm

yield strength = 350 MN/m^2

Torque ( T ) = 100 N.m

Bending moment = 150 N.m

Determine the value of the applied axial tensile force when yielding of rod occurs

first we will calculate the shear stress and normal stress

shear stress ( г ) = Tr / J = [( 100 * 10^3) * 10 ] /
`\pi /32` * ( 20)^4

= 63.662 MPa

Normal stress( Гb + Гa ) = MY/ I + P/A

= [( 150 * 10^3) * 10 ] /
`\pi /32` * ( 20)^4 + 4P /
`\pi * 20^2`

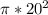
= 190.9859 + 4P /
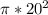`\pi * 20^2` MPa

a) Using MSS theory

value of axial force = 42.422 KN

solution attached below

b) Using MDE theory

value of axial force = 44.356 KN

solution attached below