Answer:
the period of the physical pendulum is 0.498 s
Step-by-step explanation:
Given the data in the question;
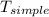 = 0.61 s
= 0.61 s
we know that, the relationship between T and angular frequency is;
T = 2π/ω ---------- let this be equation 1
Also, the angular frequency of physical pendulum is;
ω = √(mgL /
 ) ------ let this equation 2
) ------ let this equation 2
where m is mass of pendulum, L is distance between axis of rotation and the center of gravity of rod and
 is moment of inertia of rod.
is moment of inertia of rod.
Now, moment of inertia of thin uniform rod D is;
 =
=
 mD²
mD²
since we were not given the length of the rod but rather the period of the simple pendulum, lets combine this three equations.
we substitute equation 2 into equation 1
we have;
T = 2π/ω OR T = 2π/√(mgL/
 ) OR T = 2π√(
) OR T = 2π√(
 /mgL)
/mgL)
so we can use
 =
=
 mD² for moment of inertia of the rod
mD² for moment of inertia of the rod
Since center of gravity of the uniform rod lies at the center of rod
so that L =
 D.
D.
now, substituting these equations, the period becomes;
T = 2π/√(
 /mgL) OR T =
/mgL) OR T =
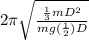 OR T = 2π√(2D/3g ) ----- equation 3
OR T = 2π√(2D/3g ) ----- equation 3
length of rod D is still unknown, so from equation 1 and 2 ( period of pendulum ),
we have;
ω
 = 2π/
= 2π/
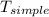 OR ω
OR ω
 = √(g/D) OR ω
= √(g/D) OR ω
 = 2π√( D/g )
= 2π√( D/g )
so we simple solve for D/g and insert into equation 3
so we have;
T = √(2/3) ×
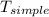
we substitute in value of
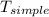
T = √(2/3) × 0.61 s
T = 0.498 s
Therefore, the period of the physical pendulum is 0.498 s