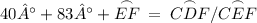Question

Can someone help me pls

Answer 1

`\boxed{ m \overset{\huge\frown}{EFC} \: = \: 237°}`

Step-by-step explanation:

Assuming that
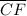`\overline{CF}` is a diameter, and that the angle of an arc subtending the central angle is congruent,
`m \overset{\Large\frown}{CGF} \: = \: 180°`.

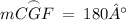And according to the arc addition postulate,
`\overset{\Large\frown}{CG} + \overset{\Large\frown}{GF} \: = \: \overset{\huge\frown}{CGF}`.

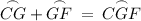Using the substitution property:

`\overset{\Large\frown}{CG} + \overset{\Large\frown}{GF} \: = \: 180°`.

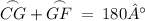Given that
`m\overset{\Large\frown}{CG} \: = \: 140°`.

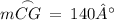Using the substitution property and that the measures apply to the arc addition postulate,
`140° + m\overset{\Large\frown}{GF} \: = \: 180°`.

`140° – \: 140° + m\overset{\Large\frown}{GF} \: = \: 180° – \: 140°`.

`m\overset{\Large\frown}{GF} \: = \: 40°`.

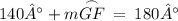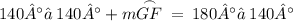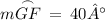Since
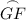`\overset{\Large\frown}{GF}` and
`\overset{\Large\frown}{CD}` are subtending the center of the circle, they form vertical angles and are therefore congruent.

`\overset{\Large\frown}{GF} \: \cong \: \overset{\Large\frown}{CD}`

According to the definition of a vertical angle,
`m \overset{\Large\frown}{CD} \: = \: 40°`.

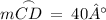Using the arc addition postulate again,

`\overset{\Large\frown}{CD} + \overset{\Large\frown}{DE} + \overset{\Large\frown}{EF} \: = \:\overset{\huge\frown}{CDF}/\overset{\huge\frown}{CEF}`

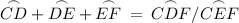
Using substitution, as well as how we are given that the central angle subtended by
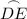`\overset{\Large\frown}{DE}` = 83°, we can find that:

`40° + 83° + \overset{\Large\frown}{EF} \: = \:\overset{\huge\frown}{CDF}/\overset{\huge\frown}{CEF}`