Let X be a random variable denoting pulse rates of females as described, with mean µ = 74.0 bpm and standard deviation σ = 12.5 bpm. Then
P(70 < X < 78) = P((70 - µ)/σ < (X - µ)/σ < (78 - µ)/σ)
… = P(-0.32 < Z < 0.32)
… = P(Z < 0.32) - P(Z < -0.32)
… ≈ 0.6255 - 0.3745
… ≈ 0.2510
where Z is normally distributed with mean 0 and s.d. 1.
• • •
Next, you sample 25 females from the population and want to find the probability that their average falls between 70 and 78 bpm. Let
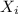 denote the pulse rate of the i-th woman from the sample, and let Y be the random variable for the sample mean; that is,
denote the pulse rate of the i-th woman from the sample, and let Y be the random variable for the sample mean; that is,
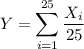
Recall that a sample of size n taken from a normal distribution with mean µ and s.d. σ has a mean that is also normally distributed with mean µ and s.d. σ/√n.
The mean stays the same, µ = 74.0, but now the s.d. is σ/√n = σ/5 = 2.5. So we have
P(70 < Y < 78) = P((70 - µ)/(σ/5) < (Y - µ)/(σ/5) < (78 - µ)/(σ/5))
… = P(-1.6 < Z < 1.6)
… = P(Z < 1.6) - P(Z < -1.6)
… ≈ 0.9452 - 0.0548
… ≈ 0.8904