Question

X 6.4.7-T

Question Help
Assume that females have pulse rates that are normally distributed with a mean of j = 74.0 beats per minute and a standard deviation of o = 12.5 beats per minute. Complete parts (a) through (c) below.
a. If 1 adult female is randomly selected, find the probability that her pulse rate is between 70 beats per minute and 78 beats per minute.
The probability is
(Round to four decimal places as needed.)
Enter your answer in the answer box and then click Check Answer
2 parts
remaining

Answer 1

Let X be a random variable denoting pulse rates of females as described, with mean µ = 74.0 bpm and standard deviation σ = 12.5 bpm. Then

P(70 < X < 78) = P((70 - µ)/σ < (X - µ)/σ < (78 - µ)/σ)

… = P(-0.32 < Z < 0.32)

… = P(Z < 0.32) - P(Z < -0.32)

… ≈ 0.6255 - 0.3745

… ≈ 0.2510

where Z is normally distributed with mean 0 and s.d. 1.

• • •

Next, you sample 25 females from the population and want to find the probability that their average falls between 70 and 78 bpm. Let
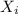`X_i` denote the pulse rate of the i-th woman from the sample, and let Y be the random variable for the sample mean; that is,

`Y=\displaystyle\sum_(i=1)^(25)(X_i)/(25)`

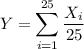
Recall that a sample of size n taken from a normal distribution with mean µ and s.d. σ has a mean that is also normally distributed with mean µ and s.d. σ/√n.

The mean stays the same, µ = 74.0, but now the s.d. is σ/√n = σ/5 = 2.5. So we have

P(70 < Y < 78) = P((70 - µ)/(σ/5) < (Y - µ)/(σ/5) < (78 - µ)/(σ/5))

… = P(-1.6 < Z < 1.6)

… = P(Z < 1.6) - P(Z < -1.6)

… ≈ 0.9452 - 0.0548

… ≈ 0.8904