Question

Consider a taut inextensible string. You shake the end of the string with some frequency, causing a wave to travel down the string. In the questions below, assume you only change one aspect of the system at a time.

1. If you shake the end of the string twice as rapidly (double the frequency), what will happen to the speed of the wave?
2. If you double the tension in the string, what will happen to the speed of the wave?
3. If you shake the end of the string twice as rapidly (double the frequency), what will happen to the wavelength of the propagating wave?
4. If you double the tension in the string, without changing the rate at which you're shaking it, what will happen to the wavelength of the wave?
For each question, choose from the following choices:
a. It will double.
b. It will remain unchanged.
c. It will increase by a factor of √ 2.
d. It will increase by a factor of 4.
e. It will be half as fast/long.

Answer 1

Part 1:

Option B is correct (It will remain unchanged).

Part 2:

Option C is correct (It will increase by a factor of √ 2)

Part 3:

Option E is correct (It will be half as fast/long.)

Part 4:

Option C is correct (It will increase by a factor of √ 2.)

Step-by-step explanation:

Formula we are going to use:

V=f*λ

Where:

V is the speed of Sound

f is the frequency of wave

λ is the wavelength.

The speed of wave , tension and linear density have following relation:

`V=√(F/\rho)`

Where:

V is the speed of Sound (Initial)

F is the tension in string (Initial)

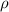`\rho` is the linear density of string (Constant)

Terms:

V' is the new speed

f' is the new frequency

λ' is the wavelength

Solution:

Part 1:

From
`V=√(F/\rho)`:

Speed of Sound is independent of the frequency of shaking so speed well remain unchanged.

Option B is correct (It will remain unchanged)

Part 2:

If F'=2F then

`V=√(F/\rho)`

`V'=√(F'/\rho)\\V'=√(2F/\rho)\\V'= √(2) * √(F/\rho)\\V'=√(2)V`

Option C is correct (It will increase by a factor of √ 2)

Part 3:

Formula we are going to use:

V=f*λ

Given f'=2f,

Even though frequency is doubled we will keep velocities same. V=V' in order to find the changing wavelength.

V'=f'*λ'

f*λ=f'*λ'

f*λ=2f*λ'

Solving above Equation:

λ'=λ/2

Option E is correct (It will be half as fast/long.)

Part 4:

T'=2T means
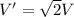`V'=√(2)V` (From Part 1)

f'=f

Now:

V'=f'*λ'

`√(2)f*\lambda=f'*\lambda '\\√(2)f*\lambda=f*\lambda '\\ \lambda '=√(2)*\lambda`

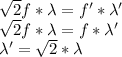
Option C is correct (It will increase by a factor of √ 2.)