Question

A national business magazine reports that the mean age of retirement for women executives is 61.7. A women’s rights organization believes that this value does not accurately depict the current trend in retirement. To test this, the group polled a simple random sample of 82 recently retired women executives and found that they had a mean age of retirement of 60.8. Assuming the population standard deviation is 4.0 years, is there sufficient evidence to support the organization’s belief at the alpha = 0.02 level of significance? State the null and alternative hypotheses for the test.

Answer 1

The calculated value |Z| = |-2.0375| = 2.0375<2.0541.96 at 0.02 level of significance

A women’s rights organization believes that the average value does not accurately depict the current trend in retirement.

Explanation:

Step(i):-

Given that the mean age of retirement for women, executives is 61.7

Given mean of the Population = 61.7

Given that the size of the sample 'n' = 82

Given that the mean of sample x⁻ = 60.8

Given that the standard deviation 'σ' = 4.0years

Step(ii):-

Null hypothesis:H₀: μ ≠ 61.7

Alternative Hypothesis: H₁: μ = 61.7

Test statistic

`Z = (x^(-) -mean)/((S.D)/(√(n) ) )`

`Z = (60.8-61.7)/((4.0)/(√(82) ) )`

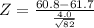
Z = -2.0375

|Z| = |-2.0375| = 2.0375< 2.054 at 0.02 level of significance

Final answer:-

The calculated value |Z| = |-2.0375| = 2.0375 <2.054 at 0.02 level of significance

A women’s rights organization believes that the average value does not accurately depict the current trend in retirement.