Question

A company categorizes its employees in three groups: I, II, and III, which constitute 20%, 60%, and 20% of the workforce respectively. Furthermore, 10%, 20%, 5% employees of group I, II, III respectively are considered certified. Given that a randomly picked employee is not certified, what is the probability that this employee belongs to group I?

Answer 1

the probability that this employee belongs to group I is 0.2118

Explanation:

Given the data in the question;

P( group 1 ) = 0.20

P( group 11 ) = 0.60

P( group 111 ) = 0.20

now

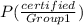`P( (certified)/(Group1) )` = 0.10

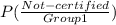`P( (Not-certified)/(Group1) )` = 0.90

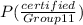`P( (certified)/(Group11) )` = 0.20

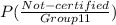`P( (Not-certified)/(Group11) )` = 0.80

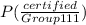`P( (certified)/(Group111) )` = 0.05

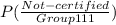`P( (Not-certified)/(Group111) )` = 0.95

so

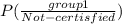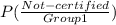`P( (group1)/(Not-certisfied) )` = [
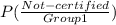`P( (Not-certified)/(Group1) )` × P( group 1 ) ] / [
`P( (Not-certified)/(Group1) )` × P( group 1 ) +
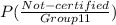`P( (Not-certified)/(Group11) )` × P( group 11 ) +
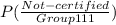`P( (Not-certified)/(Group111) )` × P( group 111 ) ]

we substitute

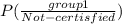`P( (group1)/(Not-certisfied) )` = [ 0.90×0.20 ] / [ 0.90×0.20 + 0.80×0.60 + 0.95×0.20

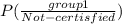`P( (group1)/(Not-certisfied) )` = 0.18 / [ 0.18 + 0.48 + 0.19 ]

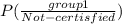`P( (group1)/(Not-certisfied) )` = 0.18 / 0.85

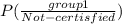`P( (group1)/(Not-certisfied) )` = 0.2118

Therefore, the probability that this employee belongs to group I is 0.2118